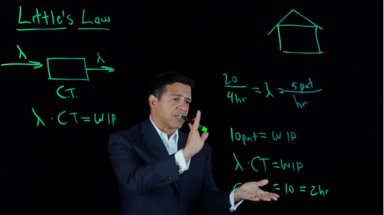At some point during the first session of our courses on Operations Management, Process Improvement, or Managing Health Care Processes we find the need to understand and utilize Little’s Law. This refers to an
observation by John Little which states that the long-term average number (L) of flow units in a stationary system is equal to the long-term average, effective arrival rate (λ) multiplied by the average time (W) that a flow unit spends in the system. Huh?
It may help if we do three things here. First, let’s translate this into English. Second, let’s restate it in a way that makes it more applicable to healthcare professionals. Third, let’s illustrate why it matters.
Let’s translate this into English
We can all recall our high school physics (or algebra) teacher who told us that (Rate) times (Time) equals (Distance). For example, 5 miles an hour for 2 hours gives 5 * 2 = 10 miles traveled. Well, Little’s Law makes a parallel claim about business processes. The Arrival Rate is how fast flow units (jobs or customers, or patients) arrive at or enter into a system. If we envision an Emergency Room (ER) and count arrivals over a 24-hour period, and we see 240 people show up at the door over this span of time, we will deduce that the average arrival rate is 240/24 = 10 people per hour. This is our Rate.
The Time dimension here refers to how long a flow unit stays within the process boundary. We will typically refer to this as Cycle Time. If patients enter the ER and stay in the waiting room for an average of 45 minutes, you might say the average Cycle Time is 45 minutes, or 0.75 hours for this process step. Given a Rate, such as 10 per hour and a Cycle Time (0.75 hours for the average stay) we can find the average number of jobs in the system, or in this setting the average number of patients in the waiting room is, 10 * 0.75 = 7.5. Rate times Time equals Distance becomes (Arrival Rate ) * (Average Cycle Time) = (Average Number of jobs in the System.)
Notice that to this point, we have applied Little’s Law to a portion of a larger process – namely waiting in the ER for further treatment. Part of the power of Little’s Law is that we could have just as easily applied the law to a different part of the process, such as time spent in an examination area of the ER. We could then apply it to the time a patient spends in the examination area waiting to be moved to a bed in another part of the hospital. We could also apply it to the total time between arrival to the ER and exit to a room or release to go home. We could even extend the logic to apply the law to the total span of time from arrival at the ER door to discharge after some time as an in-patient. The Law never changes, but the context to which it is applied has infinite variety.
Let’s put this into a relevant context
In many hospital wards we focus on the Census. This is most easily understood as the number of beds occupied. We also focus on Length of Stay, as the time between admission and discharge. Many large hospitals have a policy of not turning any patients away, so the Arrival Rate speaks for itself. Thus, we can see how (Average Census) = (Arrival Rate) * (Length of Stay). This simply restates Little’s Law for a unit of the hospital. Similarly, we could apply the law to the ER, the Operating Rooms, the Ward that houses patients, and the system as a whole. We could even extend the logic to the entire system. For example, we can look at the time between when a patient requests an appointment for a problem, to the conclusion of treatment for that condition, even though this may include multiple outpatient visits, an inpatient stay, and follow up visits. The law applies to steps, units, patient groups, and populations. We just have to be careful to define Time, Rate, and Number of flow units in a consistent way.
What can I do with this?
What’s nice about this result is that if we can find any two elements in the equation, we can figure out the third. For example, in many clinics we use a kiosk or some other automated system to record patient arrival or entry. Thus, we can look at data over some period of time and find an average arrival rate as total arrivals divided by total time. Typically, we also create a time stamp right before the patient exits the system if they follow some formal check-out process. Thus, we may have good data on Length of Stay in the facility which is the relevant Cycle Time. From these values we can find the average number of patients in a clinic, office, ward, hospital, or system at one time.
In other settings patients may exit without giving us a formal time stamp. If this happens our estimate of Length of Stay can become an unreliable value. However, if we have the arrival rate, and we periodically count the number of patients in the system to find an average Census, we can work backwards to find the average Length of Stay. Similarly, if I can find an average Length of Stay and average Census level, I can back into the average Arrival Rate.
In addition to describing or summarizing behavior for some process, Little’s Law can also help with forecasting or thinking about what will happen when a setting changes. For example if we expect the arrival rate to climb by 10% next year because the local population is growing at that rate, then we know that if we don’t change the capacity level (adjust the cycle time) we should expect to see 10% more people in our waiting room or facility on average.
Keep in mind that since the average number of jobs in the system is the product of two terms – Cycle Time and Length of Stay, a change in the average Census can have a combination of causes. For example, if arriving patients are growing in case complexity, this will tend to increase Cycle Time. If this happens, then we will see an increase in the number of patients on site even though nothing has changed in terms of our internal processes or the arrival rate. Similarly, efforts to reduce the length of stay will reduce the average number of jobs in the system, if (and only if) the arrival rate does not rise to make-up the difference. Ignoring the fact that a change to any variable interacts with two other variables simultaneously can lead to misunderstandings about what is actually going on.
Part of the beauty of Little’s Law is that it is based on averages. Thus, it works with deterministic times that are common in manufacturing, and it also works with highly variable times that we are likely to see in healthcare. This is why it forms a great starting point to begin to understand the behavior of these systems.
Take Away
Little’s Law is a great starting point for the study of many healthcare systems. More details can be found in readings that we have created for students, and a full exposition is available in Chapter 1 of our text. Check out our documents page for short readings and find us on Amazon.com for the full text.